Numerical Methods

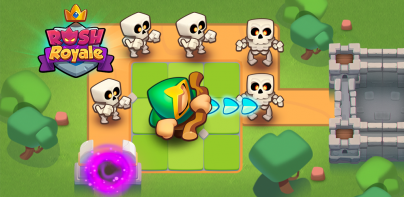
Numerikus módszerek: A hőegyenlet a Simly csúszka-alapú felületet használja, hogy megkönnyítse a hallgatók számára annak megvizsgálását, hogy a hődiffúziós problémák numerikus módszerrel történő bemeneti paramétereinek változása hogyan befolyásolja a megoldást. Bevezető anyag, vezetett vetélkedők és "lopakodó értékelések" kiegészítik a tanulási tapasztalatokat.

A hőegyenlet megoldásai a beállítható Dirichlet határfeltételekkel ellátott síkon kiszámolhatók és megmutathatók egyensúlyi és átmeneti problémákra egyaránt. Az egyensúlyi állapot megoldások megtalálhatók a véges differenciál módszerrel, Gauss-Jacobi vagy Gauss-Seidel oldószerekkel, vagy közvetlenül a véges elem módszerrel. Átmeneti megoldások az 1. rendű explicit vagy implicit megoldásokkal találhatók